Statistical Sampling
Several problems involve selecting samples with a specific objective from a pre-defined space. The optimization problem can be thought of as performing sampling such that the objective function is minimized. Another sampling problem may involve selecting training data for creating accurate machine learning models over a desired space. The sampling objective in such a scenario can be, e.g., to maximize information gain from selected samples, or to obtain a space-filling distribution of training samples. Similarly, various sampling scenarios or applications exist, including design space exploration, constrained multi-objective optimization, design space decomposition, etc. The process of sampling is known by different names in different contexts – active learning, sequential sampling, adaptive sampling, design of experiments, etc.
Selected Research
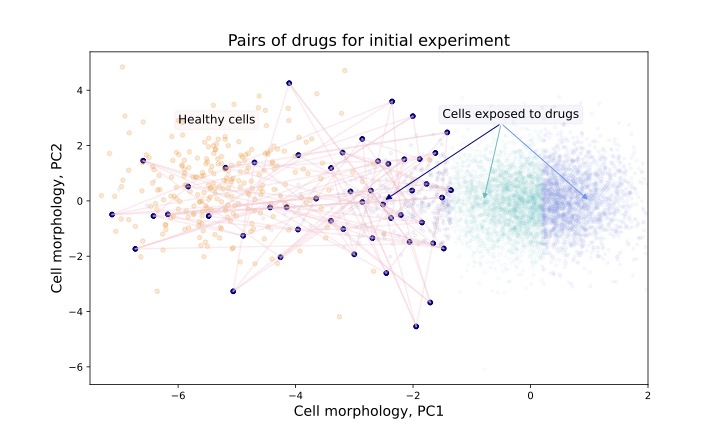
Design of Experiments for Drug Repurposing
Evaluating candidate drug compounds for efficacy towards treating a disease can be a time consuming task. The problem explodes combinatorially as the number of candidate compounds increases. There exist computational methods to help select potentially good candidates, but the large search space of several million candidate combinations is still challenging to navigate. Aleksandr Karakulev’s doctoral project aims to build a principled pipeline for efficiently finding pseudo-optimal drug compound combinations.
Two more interesting projects will be announced soon in this area.
Sampling Class Boundaries
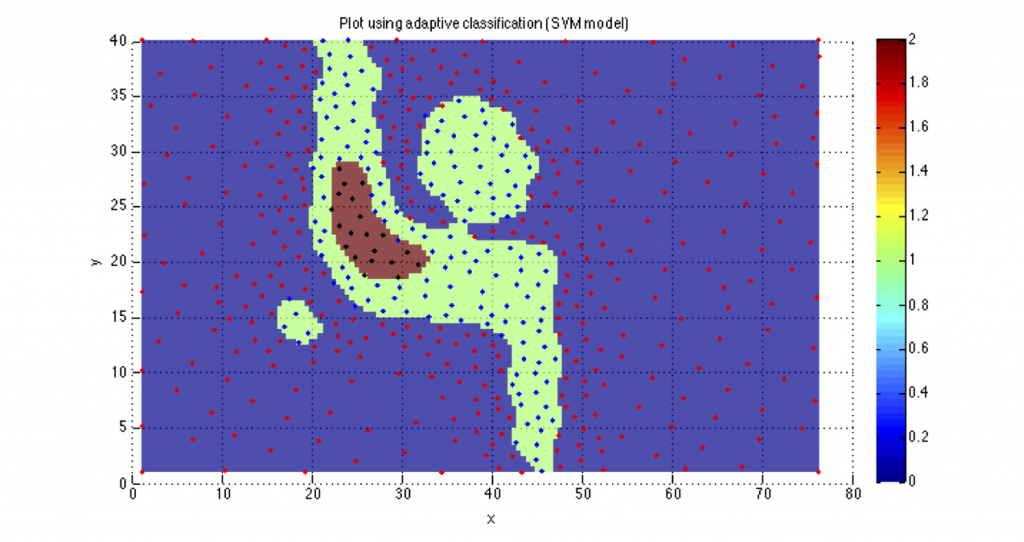
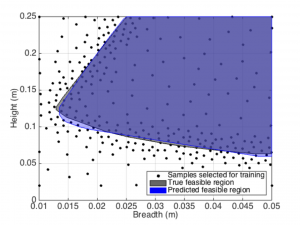
The highest uncertainty in predictions of a classifier are typically in the regions where class boundaries lie. In classification problems involving computationally expensive data (e.g., from high fidelity simulations) where one can freely sample training data, it is desirable to train an accurate classifier while minimizing the size of the training set. An intuitive approach is therefore to sample more frequently along the class boundaries, while performing space-filling sampling in the rest of the space. The Neighborhood-Voronoi algorithm [1,2] implements this strategy leveraging Voronoi tessellations. Decomposing the input space into a Voronoi tessellation, space-filling exploration can be performing in large Voronoi cells, while neighboring cells with class label disagreements form a good candidate for exploitation of areas along the class boundaries. The resulting training set enables accurate classifiers while being data-efficient.
[1] Singh, P., Van Der Herten, J., Deschrijver, D., Couckuyt, I., & Dhaene, T. (2017). A sequential sampling strategy for adaptive classification of computationally expensive data. Structural and Multidisciplinary Optimization, 55(4), 1425-1438.
[2] Singh, P., Deschrijver, D., Pissoort, D., & Dhaene, T. (2013). Adaptive classification algorithm for EMC-compliance testing of electronic devices. Electronics Letters, 49(24), 1526-1528.
Global Surrogate Modeling
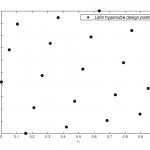
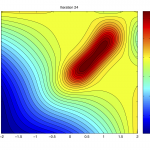
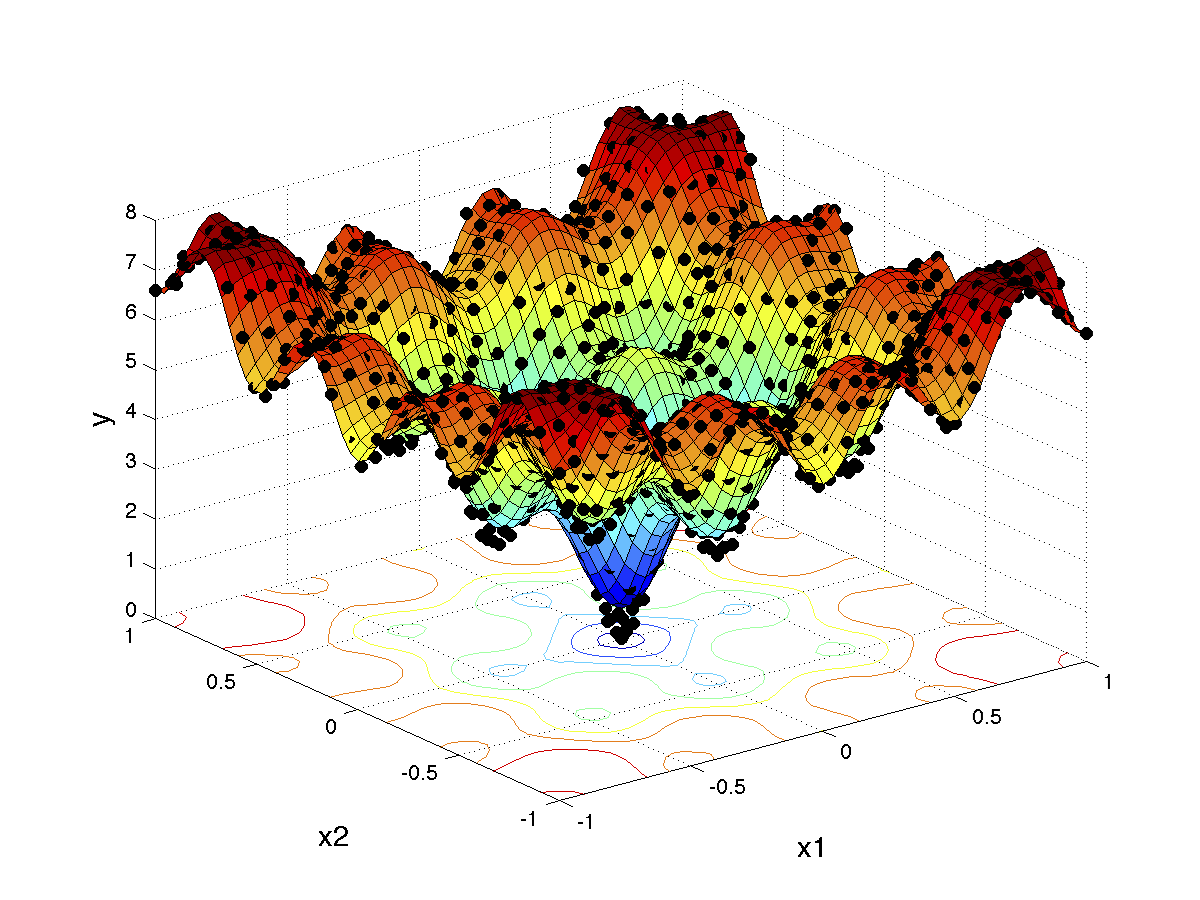
The exploration versus exploitation tradeoff is also encountered while generating training data to create globally accurate surrogate models in settings where it is possible to freely select samples (e.g., training data from simulations). Such global models are typically machine learning models and are also known as metamodels or response surface models. Surrogate models are popular as replacements of computationally expensive functions such as CFD models, responses of microwave filters, antennae etc. Since training data usually come from computationally expensive simulations, it is important to minimize the number of training samples needed to train an accurate surrogate model. A typical surrogate modeling cycle starts with a small initial design (typically space-filling such as factorial or Latin hypercube sampling) which is refined iteratively using a sequential sampling algorithm.
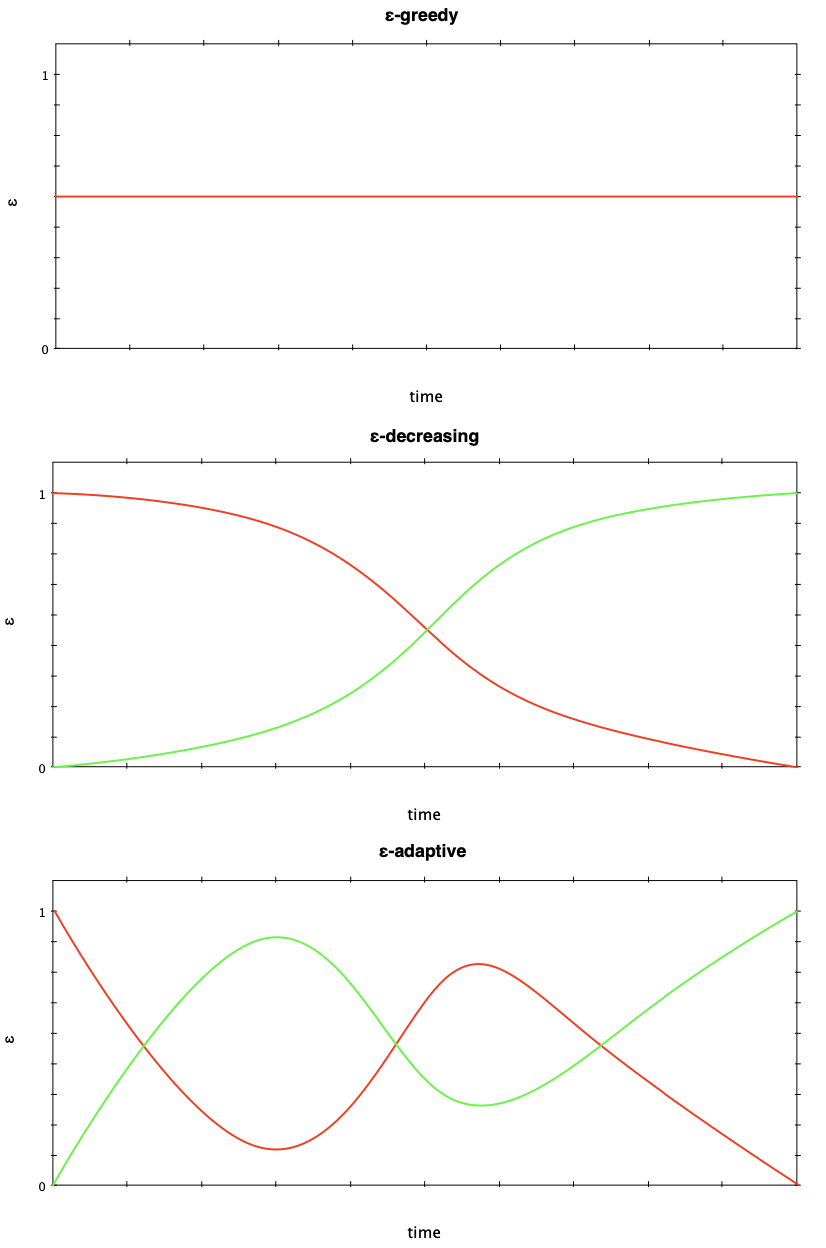
Sequential sampling must be performed at well-chosen locations such that enough samples are allocated to challenging hard-to-model highly non-linear areas. Also, space-filling exploration must be performed in order to cover the input space but samples must not be over-allocated in relatively ‘easy’ areas with flat responses. The adaptive algorithm presented in [1] uses local linear approximations to gauge the non-linearity of a particular region (the exploitation score), and Voronoi decompositions to evaluate the exploration potential of a region (the exploration score). Several strategies are evaluated to balance the contribution of each score, including a fixed 50/50 contribution, ε-greedy (exploration bias), ε-decreasing (start with full exploration as the surrogate uncertainty is high initially, and after exploring sufficiently, increase exploitation progressively) and ε-adaptive (use a metric such as the prevailing surrogate validation error to control the contribution – one can afford to exploit more if the error is low, while exploration can be performed to control high validation error). The ε-adaptive approach proved to outperform all other evaluated approaches. The algorithms presented in [1] are suitable for regression problems while the algorithm presented in [2] is suitable for global surrogate modeling of classification problems.
[1] Singh, P., Deschrijver, D., & Dhaene, T. (2013, December). A balanced sequential design strategy for global surrogate modeling. In 2013 Winter Simulations Conference (WSC) (pp. 2172-2179). IEEE.
[2] Singh, P., Van Der Herten, J., Deschrijver, D., Couckuyt, I., & Dhaene, T. (2017). A sequential sampling strategy for adaptive classification of computationally expensive data. Structural and Multidisciplinary Optimization, 55(4), 1425-1438.
Sampling with lines
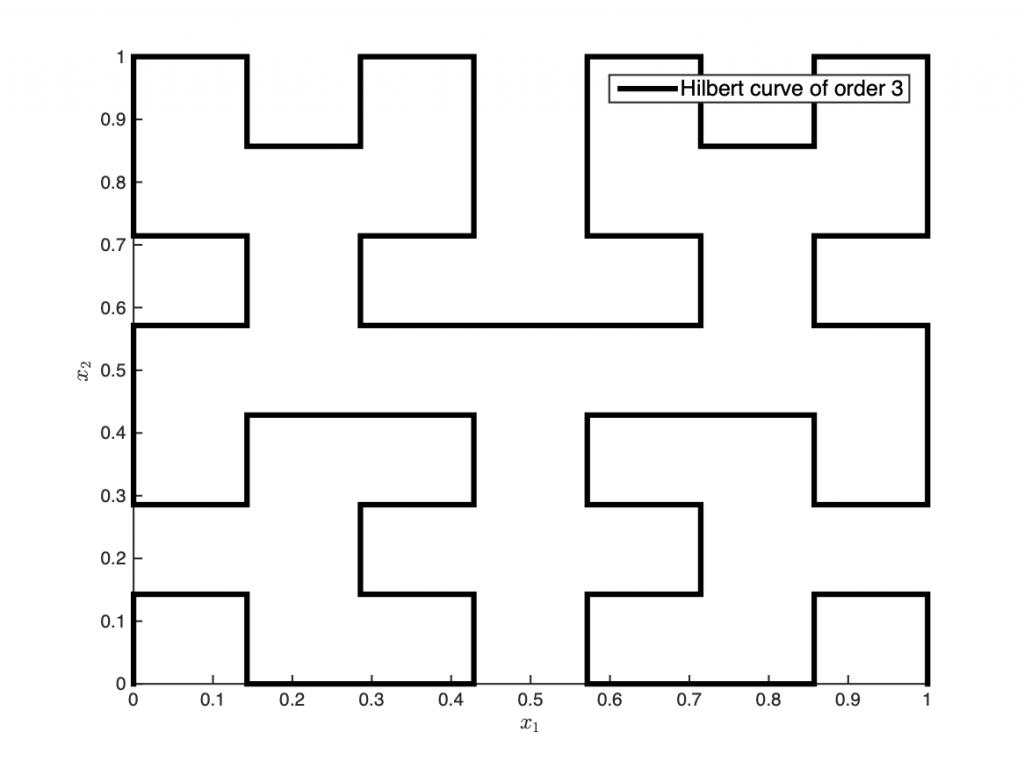
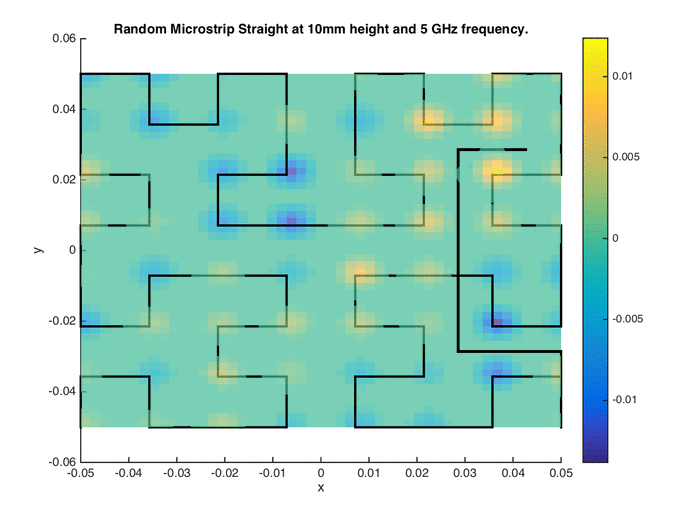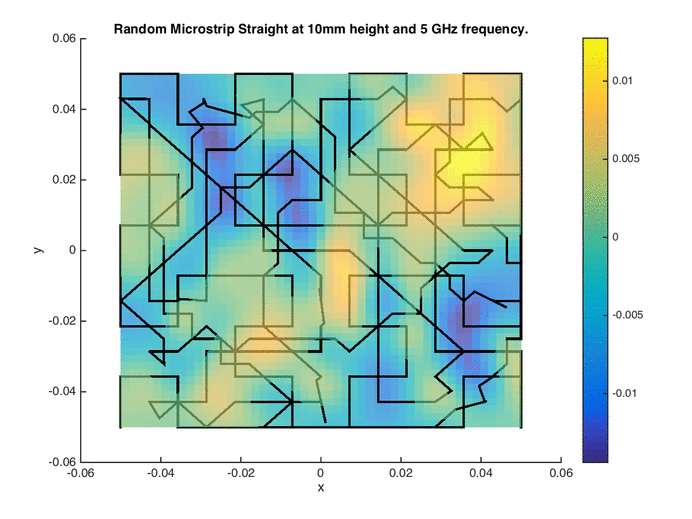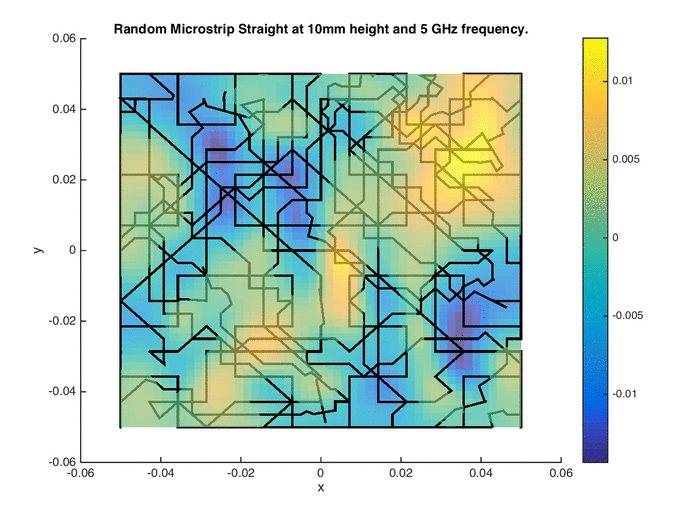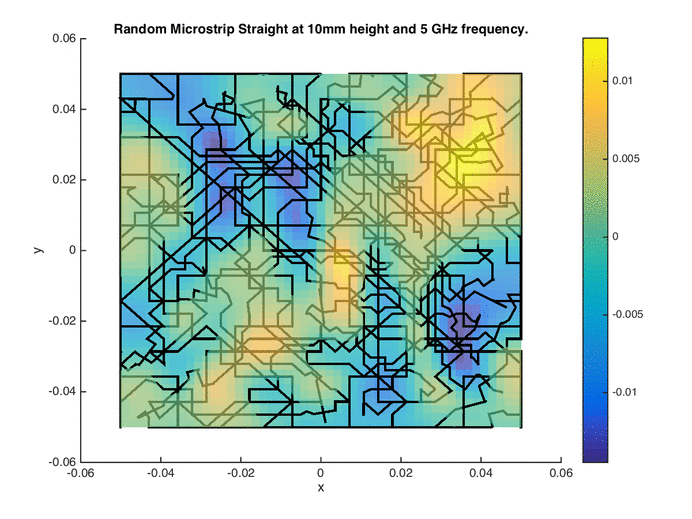
Point-based sampling can be extended a dimension further (literally) to sampling with lines. Space-filling curves have been explored in the past in the form of the Hilbert and Peano curves. These can essentially be thought of as single-shot or one-shot line-based designs. Building upon such curves as initial design, traversing the Voronoi edges of the tessellation of the initial design results in a sequential line-based space-filling design (see images on the right for the initial design and sequential sampling).
Each edge in the Voronoi tessellation can be assigned a weight, comprising of an exploration metric (proportional to the hypervolume of the Voronoi cells sharing the edge) and an exploitation metric (proportional to the non-linearity of the Voronoi cells sharing the edge). Dijkstra’s shortest path algorithm is then used to formulate a path from the current location to the destination (a location selected using the space-filling maximin criterion).
Owing to the geometry of Voronoi tessellations, the edges (and consequently the paths) can be jagged in character. Smoothing operations can yield more amenable paths based on the application. The Voronoi Edge Traversal (VET) algorithm has been successfully applied for formulating paths for near-field measurement probes [1]. The Hilbert curve as an initial design in conjunction with the global surrogate modeling algorithm described above has been used for designing wireless signal strength measurement paths for automated guided vehicles (AGVs) [2]. Measurement using drones or adaptive paths design for drones is also an interesting application area.
[1] Singh, P., Claeys, T., Vandenbosch, G. A., & Pissoort, D. (2016). Automated line-based sequential sampling and modeling algorithm for EMC near-field scanning. IEEE Transactions on Electromagnetic Compatibility, 59(2), 704-709.
[2] Gong, X., Trogh, J., Braet, Q., Tanghe, E., Singh, P., Plets, D., … & Joseph, W. (2016). Measurement-based wireless network planning, monitoring, and reconfiguration solution for robust radio communications in indoor factories. IET Science, Measurement & Technology, 10(4), 375-382.
Quasi-Optimal Regions / Hotspot Detection / The Inverse Problem
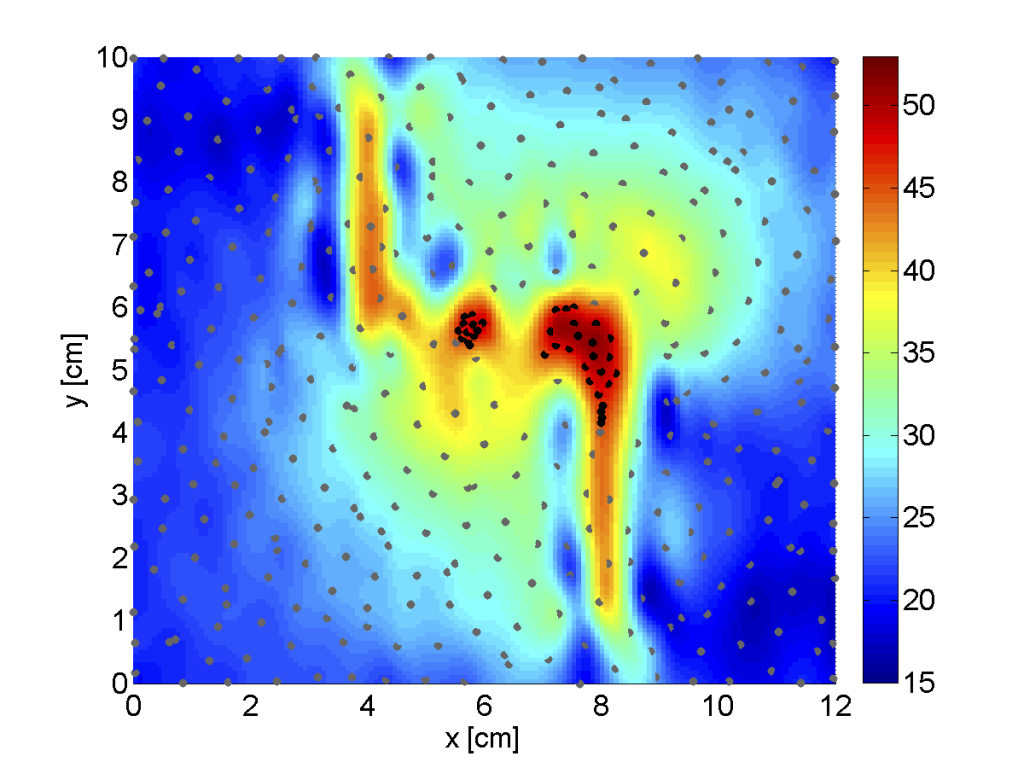
The inverse problem of inferring regions in the input space corresponding to a known output range can also be viewed as a sampling problem. The sampling algorithm must select samples in the input space with a high probability of lying in the specified/desired output range. The generalized probability of improvement (gPoI) sampling metric [1] computes the probability of a candidate sample having an output/response value within the specified range, using a PDF provided by a Gaussian process/Kriging surrogate model. Candidate samples that maximize this metric characterize the hotspot.
The inverse problem can also be cast as a classification problem. Each desired range can form a class, and then the solution of the inverse problem involves characterizing the class boundaries [2]. This can be done using an adaptive classification algorithm.
[1] Singh, P., Deschrijver, D., Pissoort, D., & Dhaene, T. (2013). Accurate hotspot localization by sampling the near-field pattern of electronic devices. IEEE Transactions on Electromagnetic Compatibility, 55(6), 1365-1368.
[2] Singh, P., Deschrijver, D., Pissoort, D., & Dhaene, T. (2013). Adaptive classification algorithm for EMC-compliance testing of electronic devices. Electronics Letters, 49(24), 1526-1528.
[3] Singh, P., Van Der Herten, J., Deschrijver, D., Couckuyt, I., & Dhaene, T. (2017). A sequential sampling strategy for adaptive classification of computationally expensive data. Structural and Multidisciplinary Optimization, 55(4), 1425-1438.